カルマン渦とは|発生の原理から可視化事例を紹介
カルマン渦とは?
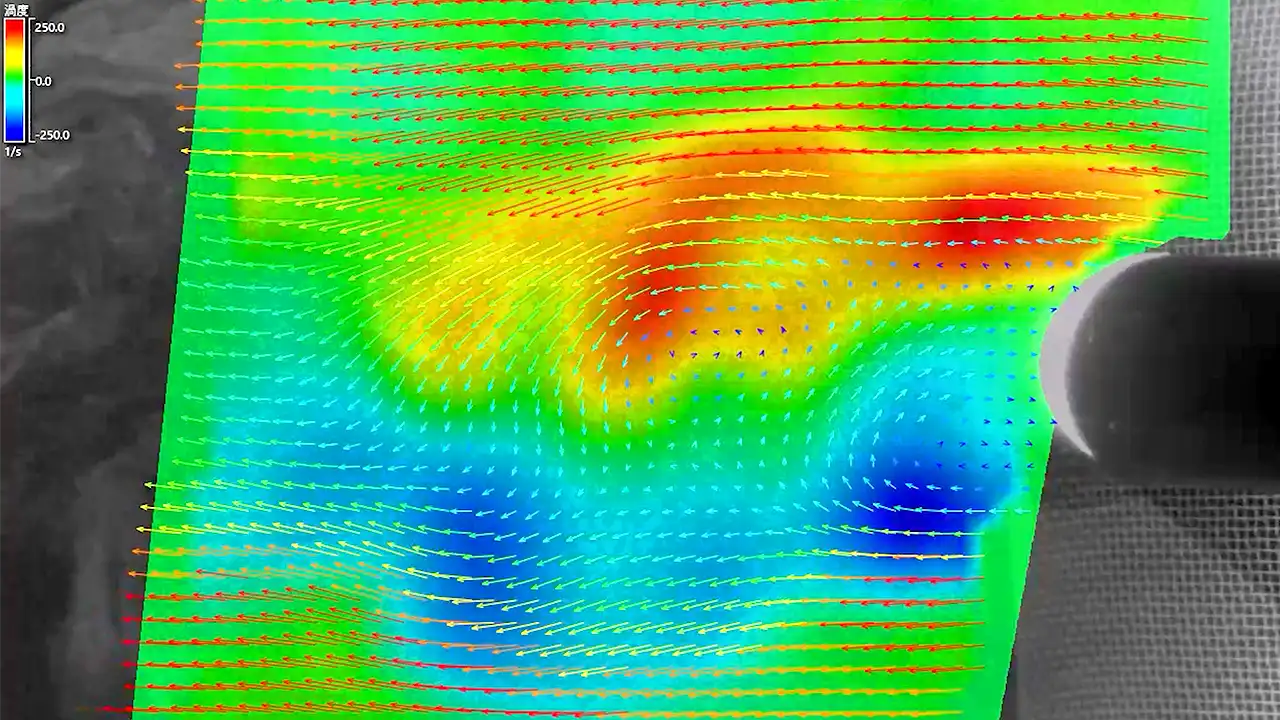
円柱後方のカルマン渦をPIVで計測した様子
カルマン渦(Kármán vortex)は、流れ場に障害物を置いたとき、その後方で周期的かつ規則正しく発生する渦の列を指します。障害物の背後に形成されるこの渦列は、流体力学における代表的な後流構造の一つであり、交互に反転しながら並ぶ渦のパターンが特徴です。
障害物後流における渦の発生メカニズム
たとえば、流れの中に円柱を置いた場合、その周囲で境界層が剥離し、左右交互に渦が剥離・放出されることで、後流に規則的なカルマン渦列が現れます。この構造は、レイノルズ数と呼ばれる無次元数の大きさによって発生のしやすさや渦の周期が決まるため、流体現象の理解や設計評価において重要です。
研究・計測の観点から見たカルマン渦
研究・実験においては、カルマン渦は単なる流れの模様ではなく、後流の不安定性や運動量輸送、圧力・力の変動に関わる物理現象として捉えられています。
流体計測技術(例:PIVなど)を用いることで、渦の生成・発展・消滅に至る挙動を定量的に捉え、速度場や渦度分布として可視化・解析することが可能になります。これは、流体力学の基礎研究から工学応用まで幅広い分野で活用されています。
フォン・カルマンによる理論的整理

セオドア・フォン・カルマン
[Theodore von Kármán (1881-1963)]
"Portrait of Theodore von Kármán" - 出典: ウィキメディア・コモンズ (Wikimedia Commons) - 画像提供: NASA
20世紀初頭、流体力学者 テオドール・フォン・カルマン は、物体後方に形成される渦列構造について理論的な解析を行い、カルマン渦が規則的に並ぶ理由を明らかにしました。それまで経験的・観察的に知られていた周期的な渦列現象に対し、力学的な安定性の観点から説明を与えた点が、この研究の大きな特徴です。
フォン・カルマンは、無限に広がる流体中に形成される渦列を理想化したモデルを用い、左右対称に並んだ渦列は不安定である一方、左右交互に配列された渦列は安定に存在し得ることを示しました。この結果により、実際の流れ場で観測される「左右交互に並ぶ渦列構造」が、偶然の産物ではなく、流体力学的に必然な構造であることが理論的に裏付けられました。
この理論的整理によって、物体後流に現れる周期的な渦列は「カルマン渦列(Kármán vortex street)」と呼ばれるようになり、非定常後流の代表的なモデルとして位置づけられました。以降、カルマン渦は、後流の不安定性や流体力の周期変動を理解するための基礎概念として、広く用いられるようになります。
フォン・カルマンの理論は、後にストローハル数やレイノルズ数と結び付けて整理され、渦放出周期と流れ条件の関係を説明する枠組みへと発展しました。現在では、実験、数値解析、可視化計測によって観測されるカルマン渦の構造は、この理論的背景を基盤として解釈されています。
わかりやすくまとめると…
カルマン渦は、流れの中に物体が存在することで生じる後流の不安定性が、規則的な渦放出という形で現れた現象です。流体は一見すると一定方向に流れているように見えますが、物体後方では境界層の剥離をきっかけとして流れが時間的に変動し、左右交互に渦が形成されます。
このように渦が左右交互に並ぶ構造は、偶然に生じているわけではありません。20世紀初頭、フォン・カルマンは、物体後流に形成される渦列について理論的な解析を行い、左右交互に配列された渦列が力学的に安定であることを示しました。これにより、実際の流れ場で観測されるカルマン渦列が、流体力学的に必然な構造であることが明らかになりました。
また、この渦放出はランダムに起こるものではなく、流速や物体の大きさ、流体の性質によって決まり、レイノルズ数を用いて整理することができます。そのためカルマン渦は、「流れが乱流へと移行する前段階」を特徴づける代表的な非定常流れとして、流体力学の理解において重要な役割を果たしています。
さらに、可視化や計測によってその構造を捉えることで、後流の状態や流れの安定性を直感的かつ定量的に把握できる点も、カルマン渦の大きな特徴です。理論で示された渦列構造を、実際の流れ場として確認できることは、カルマン渦が基礎研究から工学応用まで広く扱われている理由の一つと言えます。
カルマン渦の身近な例
カルマン渦は特別な条件下でのみ現れる現象ではなく、流れと物体が存在する環境で普遍的に発生する流体現象です。日常的なスケールで観察される現象と、実験室や数値解析で扱われる流体力学の理論が直結している点は、カルマン渦の大きな特徴と言えます。
風に揺れる構造物とカルマン渦

カルマン渦は、研究室や実験装置の中だけでなく、私たちの身の回りのさまざまな場面で発生しています。代表的な例として、煙突、電柱、アンテナ、橋のケーブルなど、風を受ける細長い構造物が挙げられます。
これらの物体の背後では、空気の流れによってカルマン渦が周期的に発生し、物体に交互の横方向力が作用します。この力が構造物の固有振動数と一致すると、目に見える揺れや振動が生じることがあります。
旗がなびく現象とカルマン渦

風に揺れる旗の動きも、カルマン渦と深く関係しています。旗や垂れ幕のような柔軟な物体が風を受けると、その背後には周期的な渦構造が形成され、流れは時間的に変動します。このとき発生する後流の非定常性が、旗を規則的になびかせる要因の一つとなります。
川や水路で見られる渦列

水中に置かれた柱や岩の背後でも、カルマン渦は容易に観察できます。流れのある川や水路で、橋脚や杭の後方に左右交互に並ぶ渦の列が形成されている様子は、カルマン渦の典型的な例です。水は空気に比べて可視化しやすいため、このような現象は流体力学の教育や基礎実験でもよく利用されています。
カルマン渦が発生する原理
物体周りの流れと境界層の形成
流体中に物体が置かれると、流れは物体表面に沿って回り込みながら進みます。このとき、物体表面近傍では流速が低下し、境界層と呼ばれる領域が形成されます。境界層内では粘性の影響が支配的となり、流れは外側の主流とは異なる挙動を示します。
物体の形状が円柱や角柱のような鈍頭形状の場合、境界層は後方まで付着し続けることができず、ある位置で表面から剥離します。この剥離が、カルマン渦発生の出発点となります。
境界層とは?
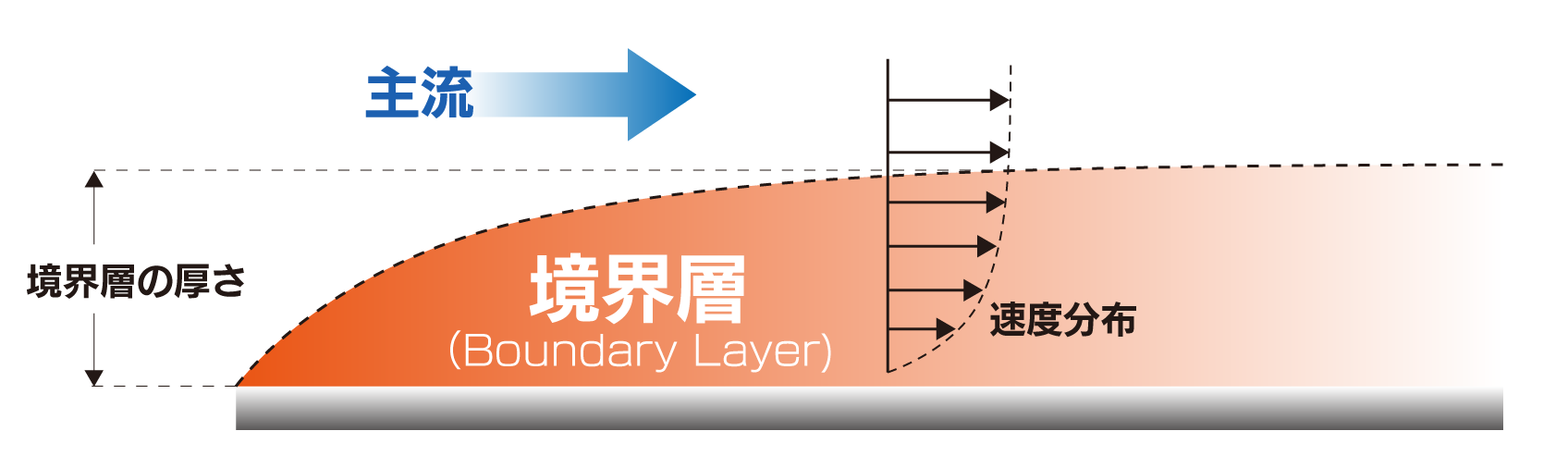
境界層とは、粘性を持つ流体(空気や水など)が物体表面に沿って流れる際に、その表面近傍に形成される非常に薄い層のことです。この層の中では、粘性による影響が大きく、流体の速度が物体表面に接する部分でゼロとなり、徐々に主流の速度へと変化していきます。
剥離せん断層の不安定化
境界層が剥離すると、物体後方には左右一対のせん断層が形成されます。これらのせん断層は、速度差を伴うため本質的に不安定であり、微小な擾乱をきっかけに波打つように変形していきます。
この不安定性の結果、片側のせん断層が巻き上がって渦を形成すると、反対側のせん断層は一時的に抑制されます。その後、逆側で同様の渦形成が起こり、左右交互に渦が放出される状態が生じます。これが、カルマン渦列の基本的な形成メカニズムです。
左右交互に渦が放出される理由
カルマン渦が左右交互に発生するのは、後流における流れ場が対称性を保てない不安定状態にあるためです。完全に対称な渦構造は力学的に不安定であり、わずかな乱れによって対称性が崩れ、結果として交互渦放出という安定した状態に遷移します。
この現象は、定常な流入条件であっても時間的に変動する流れが自発的に生じることを示しており、流体力学における非定常現象の代表例とされています。
流速・物体寸法・粘性の影響
カルマン渦の発生や渦放出の周期は、流速、物体の代表寸法、流体の粘性によって決まります。これらの影響はレイノルズ数によって整理され、特定の範囲において明瞭なカルマン渦列が形成されます。
この関係性により、後流構造は再現性の高い現象として扱うことができ、実験・数値解析・可視化のいずれにおいても、流体現象の理解を深めるための重要な対象となっています。
可視化による発生過程の理解
カルマン渦の発生過程は、煙や粒子を用いた可視化によって直感的に理解することができます。さらにPIV(粒子画像流速測定法)を用いることで、渦の生成位置、成長過程、後流全体の速度場を定量的に捉えることが可能です。これにより、理論で説明される不安定性が、実際の流れ場でどのように現れるかを明確に確認できます。
カルマン渦が発生するまでの流れ(まとめ)
1.流体中に円柱や角柱などの鈍頭物体が置かれる
↓
2.物体表面に沿って流れが回り込み、境界層が形成される
↓
3. 下流側で境界層が剥離し、左右のせん断層が生じる
↓
4. せん断層が速度差により不安定化する
↓
5. 一方のせん断層が巻き上がり、渦が形成・放出される
↓
6. 次に反対側で渦が形成され、左右交互の渦放出が起こる
↓
7. 下流に周期的なカルマン渦列が形成される
※カルマン渦は、物体後方で剥離したせん断層が不安定化し、左右交互に渦を放出することで形成される周期的な後流構造です。
カルマン渦とレイノルズ数の関係

オズボーン・レイノルズ
[Osborne Reynolds (1842-1912)]
"Presumed Portrait of Osborne Reynolds (1904)" by John Collier - 出典: ウィキメディア・コモンズ (Wikimedia Commons) - ライセンス: Creative Commons Public Domain Mark 1.0
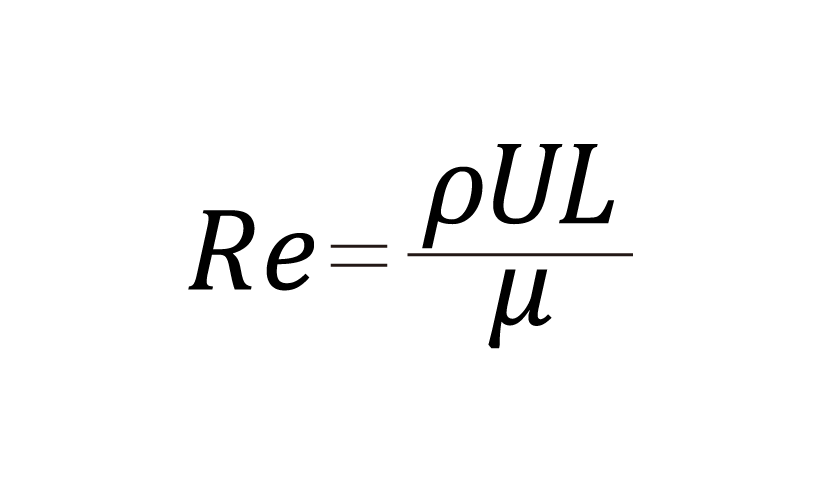
レイノルズ数の定義式
レイノルズ数は、流体の慣性力と粘性力の比を表す無次元数であり、流れの状態を分類するための基本的な指標です。流速、代表長さ、流体の密度および粘性によって決まり、同じ形状の物体であっても、レイノルズ数が異なれば流れの様相は大きく変化します。カルマン渦の発生も、このレイノルズ数に強く支配されています。
低レイノルズ数領域での流れ
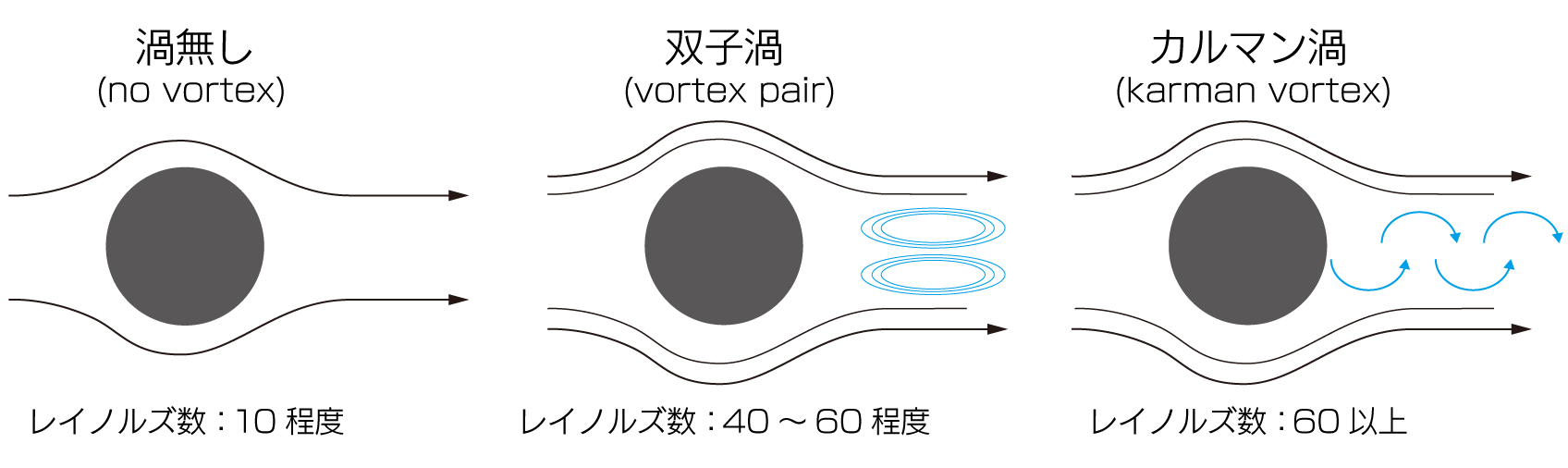
レイノルズ数が極めて小さい場合、流れは粘性の影響が支配的となり、物体後方でも流れは安定しています。この領域では、境界層の剥離は起こりにくく、周期的な渦放出は観察されません。流れは時間的にほぼ定常であり、カルマン渦は形成されない状態にあります。
カルマン渦が明瞭に現れるレイノルズ数範囲
レイノルズ数が増加すると、物体後方の流れが不安定化し、ある範囲において左右交互に渦が放出されるカルマン渦列が明瞭に現れます。この領域では、渦放出は高い周期性と再現性を持ち、流速や物体寸法を変化させても、無次元化すると同様の挙動を示します。
この性質により、カルマン渦は後流構造を整理・理解するための代表的な現象として、多くの実験や数値解析で利用されています。
高レイノルズ数領域と乱流への遷移
さらにレイノルズ数が大きくなると、カルマン渦は完全に消失するわけではありませんが、後流は次第に乱れ、渦構造は不規則になります。渦の周期性は低下し、複雑な乱流後流へと遷移していきます。
この過程は、層流から乱流への遷移を理解する上で重要であり、カルマン渦はその初期段階を特徴づける現象として位置づけられています。
可視化・計測における意義
カルマン渦とレイノルズ数の関係は、PIVなどの流体計測手法を用いることで定量的に評価することができます。異なるレイノルズ数条件下での速度場や渦度分布を比較することで、後流構造の変化や不安定性の発達過程を明確に捉えることが可能になります。
このような可視化・計測は、基礎研究のみならず、実機設計や流動評価にも広く活用されています。
カルマン渦の周期性を表すストローハル数

ヴィンチェンツ・ストローハル
[Vincenc Strouhal (1850–1922)]
“Strouhal-Vincenc_portret” by Author unknown - 出典: ウィキメディア・コモンズ (Wikimedia Commons) - ライセンス: Creative Commons Public Domain Mark 1.0
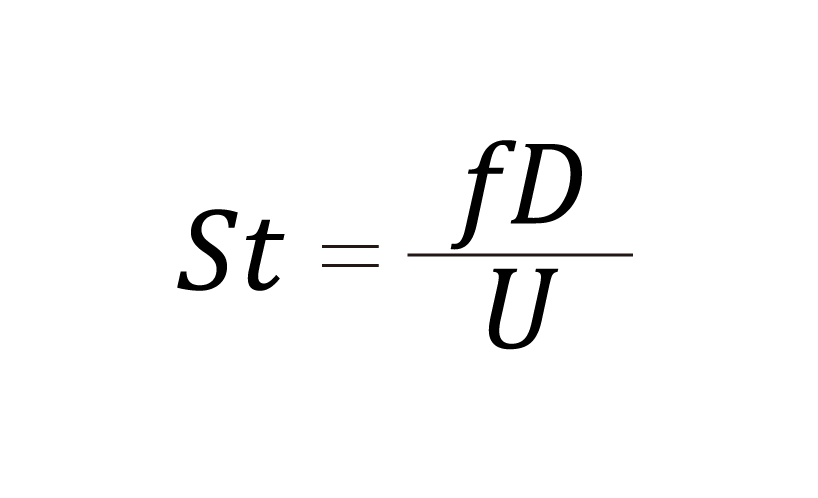
ストローハル数の定義式
St:ストローハル数
f:流れの振動の周波数[1/s]
D:代表長さ[m]
U:流速[m/s]
ストローハル数は、流れにおける周期的現象の時間スケールを表す無次元数であり、カルマン渦の渦放出周期を整理するために広く用いられています。この数は、19世紀末に物理学者 ヴィンチェンツ・ストローハル によって提唱されました。
ストローハルは、風を受けて振動するワイヤや弦の音に着目し、その振動周波数が流速や物体寸法と一定の関係を持つことを実験的に示しました。この観測結果が後に無次元化され、現在の「ストローハル数」として整理されています。
カルマン渦とストローハル数の関係
カルマン渦が安定して発生している条件下では、渦は一定の周期で規則正しく放出されます。この周期性は、流速や物体寸法が変化しても、ストローハル数として整理するとほぼ一定の値を示すことが知られています。
この性質により、ストローハル数はカルマン渦の発生状態や後流構造を評価するための、代表的な指標となっています。
周期性が示す物理的意味
ストローハル数が一定に保たれるという事実は、後流における不安定性が、特定の時間スケールで安定して繰り返されていることを意味します。すなわち、カルマン渦は偶発的に生じる乱れではなく、流れの条件に応じて自己組織化された非定常構造であることが、ストローハル数を通じて理解できます。
工学的応用と歴史的意義
ストローハル数は、カルマン渦による振動や騒音評価、さらにはカルマン渦流量計などの計測機器の原理にも応用されています。もともとは音と振動の研究から見いだされた指標が、後にカルマン渦の理論と結び付けられ、流体力学の基礎概念として定着した点は、流体研究史においても重要な意味を持っています。
カルマン渦と共振
カルマン渦が発生すると、物体の後方では渦が左右交互に周期的に放出されます。このとき、物体には時間的に変動する横方向の流体力が作用します。流れ自体は一定であっても、カルマン渦の周期性によって、物体は繰り返し押される状態となります。
この周期的な力は、流速や物体寸法によって決まるため、条件が整うと構造物の振動と強く結びつくことがあります。
共振が起こる仕組み
カルマン渦の放出周波数が、構造物の固有振動数と一致、または近い値になると、共振が生じます。振動振幅が急激に増大することが特徴です。共振状態では、わずかな流体力であっても振動が持続・増幅されるため、構造物に大きな影響を及ぼします。
固有振動数とは?
固有振動数とは、物体や構造物が外力を受けずに振動したときに、自然に現れる振動の周波数のことを指します。構造物はそれぞれ固有の質量や剛性、形状を持っており、それらの物理的特性によって、特定の振動しやすい周波数が決まっています。外部から力を加えなくても、一度変形させて手を離すと、その固有振動数で揺れ続ける点が特徴です。
●固有振動数を決める要因
固有振動数は、主に以下の要因によって決まります。
・構造物の質量
・材料や形状による剛性
・支持条件や拘束条件(固定・支持の仕方)
一般に、質量が大きいほど固有振動数は低くなり、剛性が高いほど固有振動数は高くなります。そのため、同じ形状の構造物でも、材質や支持方法が異なると固有振動数は変化します。
●流体現象との関係
流れの中に置かれた構造物では、カルマン渦のような周期的な流体力が外力として作用します。この外力の周波数が構造物の固有振動数と一致、または近づくと、共振が起こり、振動が増幅される可能性があります。そのため、固有振動数は、流体による振動や騒音、疲労評価を行う上で、非常に重要な指標となります。
カルマン渦が引き起こす現象と対策

カルマン渦が発生すると、物体の背後で左右交互に渦が放出されるため、物体には周期的に変動する横方向の流体力が作用します。この力の変動は、定常流条件下であっても発生し、物体に振動や揺れを引き起こす要因となります。
特に円柱やケーブル、配管のような細長い構造物では、この影響が顕著に現れます。
振動・騒音・疲労への影響
カルマン渦による周期的な力が構造物の固有振動数と一致すると、渦励振(Vortex Induced Vibration)と呼ばれる現象が生じます。この状態では振動振幅が増大し、騒音の発生や、長期的には材料の疲労破壊につながる可能性があります。とくに橋梁ケーブル、煙突、熱交換器の管群などでは、設計段階からこの影響を考慮する必要があります。
流動機能への影響
カルマン渦は、振動や騒音といった負の側面だけでなく、流れの状態を特徴づける現象としても重要です。後流の非定常性が強まることで、圧力損失の増加や混合特性の変化が生じる場合があります。一方で、この周期性を利用し、流量計測などに応用されている例もあります。
カルマン渦への代表的な対策
カルマン渦は、橋梁ケーブル、煙突、鉄塔、アンテナなどの構造物に周期的な流体力を与え、振動や騒音の原因となることがあります。そのため、工学分野ではカルマン渦の発生条件や渦放出周波数を把握し、共振を避ける設計や振動抑制対策を講じることが重要です。
カルマン渦による影響を抑制するためには、後流における周期的な渦放出を弱める、あるいは規則性を崩す対策が有効です。代表的な方法としては、以下が挙げられます。
① 形状最適化による渦発生の抑制
物体形状を変更することで、境界層の剥離位置や剥離の仕方を制御し、カルマン渦の発生そのものを弱めます。角の面取りや断面形状の変更などにより、後流の規則的な渦形成を抑制できます。
② 表面構造による周期性の分断
物体表面にスパイラルフィンや突起を設けることで、渦の発生タイミングや成長過程を乱し、左右交互に発生する周期性を崩します。これにより、カルマン渦に起因する力の変動を低減できます。
③ 配置工夫による後流干渉の活用
複数の物体を配置する場合には、間隔や配置を工夫することで後流同士を干渉させ、安定したカルマン渦列の形成を妨げます。管群や支持構造物などで用いられる代表的な対策です。
④ 構造設計による共振回避
流体側の対策だけでなく、構造物側の剛性や減衰特性を調整し、カルマン渦の放出周波数と固有振動数が一致しないよう設計することも重要です。これにより、渦励振(VIV)による振動増幅を防止できます。
カルマン渦の工業・産業分野での活用例
配管・熱交換器など流体機器への影響評価
配管や熱交換器の管群では、カルマン渦による流体力の変動が、振動や摩耗、長期的な疲労損傷につながる場合があります。これらの装置では、管径や配置間隔を調整し、安定した渦列が形成されにくい条件を選定することが行われています。カルマン渦の理解は、流体機器の信頼性向上と長寿命化に直結します。
計測技術への応用(カルマン渦流量計)
カルマン渦の周期性は、流量計測にも応用されています。物体後方で発生する渦の放出周波数が流速に比例する性質を利用したカルマン渦流量計は、液体や気体の流量を安定して測定できる手法として広く用いられています。
このように、カルマン渦は制御すべき現象であると同時に、積極的に利用される現象でもあります。
空力・水力設計への活用
航空機、車両、船舶などの分野では、カルマン渦を含む後流構造の理解が、空気抵抗や流体抵抗の低減、安定性向上につながります。模型実験や数値解析と併せて可視化・計測を行うことで、設計案ごとの後流特性を比較し、最適な形状を検討することが可能です。
可視化・計測技術による設計支援
PIVなどの流体可視化・計測技術を用いることで、カルマン渦の発生位置、周期性、後流全体の速度場を定量的に把握できます。これにより、設計段階での課題抽出や対策効果の検証が容易になり、試行錯誤の効率化につながります。
工学・産業分野において、カルマン渦の可視化は設計判断を支える重要な手段となっています。
カルマン渦のPIV計測例
カルマン渦の実測をPIV解析【円柱後方の気流】
使用製品
- PIV Laser Fiber Spectra(ファイバーレーザー)
- ハイスピードカメラk5(2台)
- PIVソフトFlowExpertⅡ2D3C
カルマン渦をステレオPIVで解析。円柱後方で発生したカルマン渦をステレオPIV(2次元3成分)で解析して、速度ベクトルを算出しました。レーザーシート光源で可視化されたカルマン渦を2台のハイスピードカメラで撮影して解析した結果をご紹介します。
ステレオPIVシステム2D3C(2次元3成分PIV)
ステレオ撮影で速度3成分(U,V,W)を高精度に測定
信頼性の高い流体計測手法として実績があるステレオPIV(粒子画像流速測定法)を、最新の技術でさらに高精度に。ステレオPIVシステム2D3Cは、様々な流体解析のニーズに応えます。2台のハイスピードカメラにより、3成分速度データ(U, V, W)を正確に測定することができ…製品ページを見る
流体シミュレーションで再現 カルマン渦のPIV計測
流体シミュレーションとCGを使って、障害物の後方でカルマン渦を発生させています(レイノルズ数 Re=105を想定) CGの流体にトレーサー粒子を追従させて、PIV計測を行いました。粒子の移動量から瞬時速度を算出し、渦度・速度分布を表示させています。
PIVシステム2D2C(2次元2成分PIV)
非接触で2次元断面の速度(U,V)を算出
流速計では観測空間に接触して1点で1成分計測になるのに対し、PIVでは非接触で2次元断面のエリア2成分(X, Y)の速度評価を時系列で行うことができます。CW(連続発振)レーザーシート光源とハイスピードカメラを組み合わせることで、従来のダブルパルスレーザーによる構成よりも扱いやすく…製品ページを見る
カルマン渦についての質問
- カルマン渦ができる条件は?
-
カルマン渦は、流れの中に円柱や角柱などの障害物があり、
その後方で流れが剥離して不安定になる条件下で発生します。
特に、流速、物体の大きさ、流体の粘性によって決まるレイノルズ数が一定の範囲にあるとき、
物体後流で左右交互に規則正しい渦放出が生じ、カルマン渦列が形成されます。また、物体の形状が鋭利でなく、境界層が剥離しやすい「鈍頭形状」であることも重要な条件です。
レイノルズ数が小さすぎる場合は流れが安定し、逆に大きすぎる場合は後流が乱流化して、
明瞭な周期性を持つカルマン渦は観察されにくくなります。※鈍頭形状(どんとうけいじょう)とは、流れに対して先端が鋭くなく、丸みや平らな面を持つ形状のことを指します。
代表的な例としては、円柱、角柱、角の立った柱状物体などが挙げられます。このような形状では、流体が物体表面に沿って流れ続けることができず、
途中で境界層が剥離しやすいという特徴があります。その結果、物体の後方に不安定な後流が形成され、
カルマン渦のような周期的な渦構造が発生しやすくなります。一方、流線型のように先端が鋭く後方に向かって滑らかに絞られた形状では、流れの剥離が起こりにくく、
明瞭なカルマン渦は形成されにくくなります。
- レイノルズ数がいくつになるとカルマン渦が発生しますか?
-
一般に、円柱などの鈍頭物体まわりの流れでは、レイノルズ数がおよそ 40~50 を超えると、
物体後方で周期的な渦放出が始まり、カルマン渦が発生します。レイノルズ数がこれより小さい場合、流れは粘性の影響が強く、
物体後流でもほぼ定常な状態が保たれます。
一方、レイノルズ数が増加して 100~数千程度の範囲では、
左右交互に規則正しいカルマン渦列が明瞭に観察されます。さらにレイノルズ数が大きくなると、後流は次第に乱流化し、渦構造は不規則になります。
この場合でも渦放出自体は起こりますが、周期性は弱まり、
典型的なカルマン渦列としては捉えにくくなります。Re ≲ 40:定常流(カルマン渦は発生しない)
Re ≈ 40~数千:周期的なカルマン渦が明瞭に発生
Re ≫ 数千:後流が乱流化し、周期性が不明瞭になる※実際の発生条件は、物体形状や表面状態、流れの乱れ強さによって多少変化します。
- 双子渦とカルマン渦の違いは何ですか?
-
双子渦とカルマン渦の大きな違いは、流れが定常か非定常か、そして渦が固定されているか、
周期的に放出されるかにあります。双子渦は、物体後方に左右対称に形成される一対の渦で、
比較的低いレイノルズ数条件下で観察されます。
この渦は物体背後にほぼ固定された状態で存在し、時間的な変動が小さいことが特徴です。
流れ全体は定常的で、渦が周期的に下流へ流れ去ることはありません。一方、カルマン渦は、レイノルズ数がさらに大きくなった条件で発生し、
物体後方から左右交互に渦が周期的に放出されます。
このため、流れは本質的に非定常となり、後流には規則正しい渦列(カルマン渦列)が形成されます。双子渦
・低レイノルズ数領域で発生
・左右対称な渦が物体後方に固定
・流れは定常的カルマン渦
・より高いレイノルズ数領域で発生
・渦が左右交互に周期的に放出
・流れは非定常で周期性を持つ
- 気象現象におけるカルマン渦はどういったものですか?
-
気象現象におけるカルマン渦とは、山や島などの地形が風を遮ることで、
その風下側に大気中のカルマン渦列が形成される現象を指します。
特に、孤立した島や山岳地形の背後で、雲が左右交互に並ぶ特徴的なパターンとして
観測されることがあります。代表的な例としては、海上の島の風下に発生する雲の渦列が挙げられます。
安定した風が一定方向に吹き、大気の成層が比較的安定している条件下では、
地形の背後で大気の流れが剥離し、規則正しい渦が長距離にわたって形成されます。この現象は、流体力学で扱われるカルマン渦と同じ原理に基づいており、
島や山が「鈍頭物体」として働き、大気という流体中で後流の不安定性が現れたものと理解できます。
スケールは数キロメートルから数百キロメートルに及ぶこともあり、
衛星画像によって明瞭に確認できる点が特徴です。
- カルマン渦式流量計とはどういったものですか?
-
カルマン渦式流量計とは、流体中に設置した物体の背後で発生するカルマン渦の周期性を利用して、
流量を測定する流量計です。流れの中に渦発生体(ブロック)を設置すると、
その後方でカルマン渦が左右交互に発生し、
この渦放出の周波数が流速に比例する性質を利用して流量を求めます。渦の発生周波数は、物体寸法と流速によって決まり、ストローハル数を用いて整理できます。
そのため、流体の密度や温度変化の影響を受けにくく、安定した計測が可能である点が特徴です。
カルマン渦に関連する技術コラム
【関連記事】
流れの可視化とは|歴史から手法まで解説【技術コラム】
流れの可視化は、流体の動きや特性を視覚的に捉えるための技術や手法を総称したものです。流体の動きを直接目で確認することは難しいため、この技術は流体の挙動を理解し、それを基に...「流れの可視化とは」続きを読む
【関連記事】
PIVとは|原理や計測のメリット・トレーサー粒子について解説【技術コラム】
PIVは、Particle Image Velocimetryの略で粒子画像流速測定法を意味し、流れ場における多点の瞬時速度を非接触で得ることができる流体計測法になります。流れ場の空間的な構造を把握することができるため...「PIVとは」続きを読む
【関連記事】
風洞|実験の目的から応用分野・可視化事例まで紹介【目的・用途別の可視化技術】
風洞とは人工的に発生させた空気の流れを利用して、物体に働く力やその周囲の空気の動きを精密に測定するための装置または施設です。大型のファンで空気を送り出し...「風洞|実験の目的から応用分野・可視化事例まで紹介」続きを読む
ハイスピードカメラ-製品ラインナップ
ハイスピードカメラの製品ラインナップ一覧です。人間の目では捉えきれない高速現象を克明に可視化し、解析ソフトウェアを組み合わせることで、様々な物理現象を数値化。ハイスピードカメラは研究開発・生産分野の発展...「ハイスピードカメラ製品ラインナップ」詳細ページ
製品に関するお問い合わせや技術相談を当社スタッフがお受けいたします。
※お電話でも受け付けております。
☎0463-91-1281
9:00~18:00(土日祝日を除く)